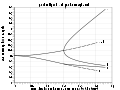
English: A plot of the long (a), middle (b) and polar (c) semi-principal axes of a Jacobi ellipsoid and Maclaurin spheroid (spinning bodies of homogeneous self-gravitating fluid in equilibrium), against normalized angular momentum, subject to abc = 1 (i.e. for constant volume of 4π/3).
The broken lines are for the Maclaurin spheroid in the range where it has dynamic but not secular stability - it will relax into the Jacobi ellipsoid provided it can dissipate energy by virtue of a viscous constituent fluid.
The lines for the Jacobi ellipsoid _go_beyond_ the point where the piriform (pear-shaped) equilibrium body could exist. According to Cartan the Jacobi ellipsoid loses all stability at this point. However, it unclear how this is to be reconciled with the fact that the piriform body is itself unstable and has a higher energy than the ellipsoid (see Christodoulou, "Phase-Transition Theory of Instabilities. III. The Third-Harmonic Bifurcation on the Jacobi Sequence and the Fission Problem", https://arxiv.org/abs/astro-ph/9505008 ).
The plot was obtained by finding c to satisfy:
a² b² (RJ(a², b², c², a²) - RJ(a², b², c², b²)) / (b² - a²) = c² RJ(a², b², c², c²)
for a and b in any given ratio (excluding a = b), and then scaling a, b and c to make abc = 1. RJ(x, y, z, p) is one of Carlson's elliptic integral functions. Having a, b and c, the corresponding normalized angular momentum was calculated according to:
L/√(rGM³) = (a² + b²) √( (a² RJ(a², b², c², a²) - b² RJ(a², b², c², b²)) / ((a² - b²)r) ) / 5
where r is the 'mean radius' = ³√(abc) = 1.
The results were checked against the tabulated values of: Poisson, Eric & Will, Clifford M. "Gravity: Newtonian, Post-Newtonian, Relativistic", p101,
https://books.google.co.uk/books?id=PZ5cAwAAQBAJ&lpg=PA103&dq=jacobi%20ellipsoid&pg=PA101#v=onepage&q=jacobi%20ellipsoid&f=false
noting that L and ω are related by:
L = Iω
I = M (a² + b²) / 5
M = 4πabcρ / 3
.











You must be logged in to post a comment.