Triakis octahedron	Tetrakis hexahedron
Deltoidal icositetrahedron	Pentagonal icositetrahedron

In geometry, an icositetrahedron^[1] refers to a polyhedron with 24 faces, none of which are regular polyhedra. However, many are composed of regular polygons, such as the triaugmented dodecahedron and the disphenocingulum. Some icositetrahedra are near-spherical, but are not composed of regular polygons. A minimum of 14 vertices is required to form a icositetahedron.^[2]

There are many symmetric forms, and the ones with highest symmetry have chiral icosahedral symmetry:

Four Catalan solids, convex:

• Triakis octahedron - isosceles triangles
• Tetrakis hexahedron - isosceles triangles
• Deltoidal icositetrahedron - kites
• Pentagonal icositetrahedron - pentagons

27 uniform star-polyhedral duals: (self-intersecting)

• Small rhombihexacron, Great rhombihexacron
• Small hexacronic icositetrahedron, Great hexacronic icositetrahedron
• Great deltoidal icositetrahedron
• Great triakis octahedron

Examples with lower symmetry include certain dual polyhedra of Johnson solids , such as the gyroelongated square bicupola and the elongated square gyrobicupola.

Common examples include prisms and pyramids, and include certain Johnson solids and Catalan solids.

Icositrigonal pyramids are a type of cone with an icositrigon as a base, with 24 faces, 46 edges, and 24 vertices.^[3] Regular icositrigonal pyramids have a regular icositrigon as a base, and its Schläfli symbol is {}∨{23}. The surface area and volume with side length and height can be calculated as follows:^[3]

Icosidigonal prisms are a type of cylinder with an icosidigon as a base, with 24 faces, 66 edges, and 44 vertices.^[4] Regular icosidigonal prisms have a regular icosidigon as a base, with each face a rectangle. Every vertex borders 2 squares and an icosidigon base. Its vertex configuration is , its Schläfli symbol is {22}×{} or t{2,22}, its Coxeter diagram is , and its Conway polyhedron notation is P22. The surface area and volume with side length and height can be calculated as follows:

Hendecagonal antiprisms are antiprisms with a hendecagon as a base, with 24 faces, 44 edges, and 22 vertices. Regular hendecagonal antiprisms have a regular hendecagon as a base, with each face an equilateral triangle. Every vertex borders 2 triangles and a hendecagon base. Its vertex configuration is .

Dodecagonal trapezohedra are the tenth member of the trapezohedra family, made of 24 congruent kites arranged radially. Every dodecagonal trapezohedron has 24 faces, 28 edges, and 26 vertices. There are two types of vertices, ones bordering 12 kits and ones bordering 3. Its dual polyhedron is the Hendecagonal antiprism.^[5] Its Schläfli symbol is { }⨁{12}, its Coxeter diagram is or , and its Conway polyhedron notation is dA12.

Dodecagonal trapezohedra are isohedral figures.

There are two examples of Johnson solids which are icositetrahedra. They are listed as follows:

Name	Image	Designation	Vertices	Edges	Faces	Types of faces	Symmetry group	Net
Disphenocingulum		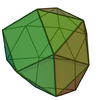J90	16	38	24	20 equilateral triangle, 4 squares	D2d
Triaugmented dodecahedron		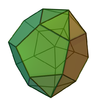J61	23	45	24	15 equilateral triangles, 9 pentagons	C3v

There are 5 types of icositetrahedra with different topologies.^[6] The pentagonal icositetetrahedron has two mirror images (enantiomorphs), so geometrically there are 4 distinct Catalan icositetetrahedra.

Name	Image	Net	Dual	Faces	Edges	Vertices	Face Configuration	Point Group
Triakis octahedron	(animation)		Truncated cube	24	36	14	Isosceles triangle V3.8.8	Oh
Tetrakis hexahedron	(animation)		Truncated octahedron	24	36	14	Isosceles triangle V4.6.6	Oh
Deltoidal icositetrahedron	(animation)		Rhombicuboctahedron	24	48	26	Kite V3.4.4.4	Oh
Pentagonal icositetrahedron	(animation) (animation)		Snub cube	24	60	38	irregular pentagon V3.3.3.3.4	O

Some uniform star polyhedra also have 24 faces:

Name	Image	Wythoff symbol	Vertex figure	Symmetry group	Faces	Edges	Vertices	Euler characteristic	Density	Faces by sides
Ditrigonal dodecadodecahedron		3 | 5/3 5	(5.5/3)3	Ih	24	60	20	-16	4	12{5}+12{5/2}
Dodecadodecahedron		5 5/2	5.5/2.5.5/2	Ih	24	60	20	-16	4	12{5}+12{5/2}
Truncated great dodecahedron		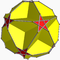2 5/2 | 5	10.10.5/2	Ih	24	90	60	-6	3	12{5/2}+12{10}
Small stellated truncated dodecahedron		2 5 | 5/3	10/3.10/3.5	Ih	24	90	60	-6	9	12{5}+12{10/3}

Name	Type	Image	Identifier	Faces	Edges	Vertices	Euler characteristic	Types of faces	Symmetry	Net
Icosidigonal prism	Prism		t{2,22} {22}x{}	24	66	44	2	2 icosidigons, 22 squares	D22h, [22,2], (*22 2 2), order 88
Icositrigonal pyramid	Pyramid		( )∨{23}	24	46	24	2	1 icositrigon, 23 triangles	C23v, [23], (*23 23)
Icosidigonal frustum	Frustum			24	66	44	2	2 icosidigons, 22 trapezoids	D22h, [22,2], (*22 2 2), order 88
Dodecagonal bipyramid	Bipyramid		{ } + {12}	24	36	14	2	12 triangles	D12h, [12,2], (*2 2 12), order 48
Dodecagonal trapezohedron	Trapezohedron		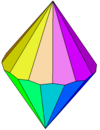{ }⨁{12}[7]	24	48	26	2	24 kites	D12d, [2+,12], (2*12)
Hendecagonal antiprism	Antiprism		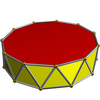s{2,22} sr{2,11}	24	44	22	2	2 hendecagons, 22 triangles	D11d, [2+,22], (2*11), order 44
Hendecagonal cupola	Cupola			24	55	33	2	11 equilateral triangles, 11 squares, 1 regular hendecagon, 1 regular icosidigon	D11d, [2+,22], (2*11), order 44
Deltoidal icositetrahedron	Johnson solid			24	48	26	2	24 kites	D4d

• Icositetragon

• Weisstein, Eric W. "Icositetrahedron". MathWorld.