a is the clockwise rotation
and b the horizontal reflection.
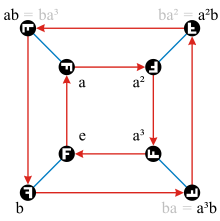
In mathematics, D4 (sometimes alternatively denoted by D8) is the dihedral group of degree 4 and order 8. It is the symmetry group of a square.[1][2]
Symmetries of a square
As an example, we consider a glass square of a certain thickness with a letter "F" written on it to make the different positions distinguishable. In order to describe its symmetry, we form the set of all those rigid movements of the square that do not make a visible difference (except the "F"). For instance, if an object turned 90° clockwise still looks the same, the movement is one element of the set, for instance a. We could also flip it around a vertical axis so that its bottom surface becomes its top surface, while the left edge becomes the right edge. Again, after performing this movement, the glass square looks the same, so this is also an element of our set and we call it b. The movement that does nothing is denoted by e.
Given two such movements x and y, it is possible to define the composition x ∘ y as above: first the movement y is performed, followed by the movement x. The result will leave the slab looking like before.
The set of all those movements, with composition as the operation, forms a group. This group is the most concise description of the square's symmetry.
Generating the group
Applying two symmetry transformations in succession yields a symmetry transformation. For instance a ∘ a, also written as a2, is a 180° degree turn. a3 is a 270° clockwise rotation (or a 90° counter-clockwise rotation). We also see that b2 = e and also a4 = e. A horizontal flip followed by a rotation, a ∘ b is the same as b ∘ a3. Also, a2 ∘ b is a vertical flip and is equal to b ∘ a2.
The two elements a and b generate the group, because all of the group's elements can be written as products of powers of a and b.
This group of order 8 has the following Cayley table:
| ∘ | e | b | a | a2 | a3 | ab | a2b | a3b |
|---|---|---|---|---|---|---|---|---|
| e | e | b | a | a2 | a3 | ab | a2b | a3b |
| b | b | e | a3b | a2b | ab | a3 | a2 | a |
| a | a | ab | a2 | a3 | e | a2b | a3b | b |
| a2 | a2 | a2b | a3 | e | a | a3b | b | ab |
| a3 | a3 | a3b | e | a | a2 | b | ab | a2b |
| ab | ab | a | b | a3b | a2b | e | a3 | a2 |
| a2b | a2b | a2 | ab | b | a3b | a | e | a3 |
| a3b | a3b | a3 | a2b | ab | b | a2 | a | e |
For any two elements in the group, the table records what their composition is. Here we wrote "a3b" as a shorthand for a3 ∘ b. This group has 5 conjugacy classes, they are .
In mathematics this group is known as the dihedral group of order 8, and is either denoted Dih4, D4 or D8, depending on the convention. This is an example of a non-abelian group: the operation ∘ here is not commutative, which can be seen from the table; the table is not symmetrical about the main diagonal.
There are five different groups of order 8. Three of them are abelian: the cyclic group C8 and the direct products of cyclic groups C4×C2 and C2×C2×C2. The other two, the dihedral group of order 8 and the quaternion group, are not.[3]
Permutation representation
The action of a rotation or diagonal reflection on the corners of a square, numbered consecutively, can be obtained by the two permutations (1234) and (13), respectively. As the positions of all four corners uniquely determine the element of the symmetries of the square used to obtain those positions, and so the group of symmetries of a square is isomorphic to the permutation group generated by (1234) and (13).
Matrix representation
The symmetries of an axis-aligned square centered at the origin can be represented by signed permutation matrices, acting on the plane by multiplication on column vectors of coordinates . The identity transformation is represented by the identity matrix . Reflections across a horizontal and vertical axis are represented by the two matrices and , respectively, and the two diagonal reflections are represented by the matrices and . Rotations clockwise by 90°, 180°, and 270° are represented by the matrices , , and , respectively. The group composition operation is represented as matrix multiplication. Larger signed permutation matrices represent in the same way the hyperoctahedral groups, the groups of symmetries of higher dimensional cubes, octahedra, hypercubes, and cross polytopes.[4]
![{\displaystyle {\bigl [}{\begin{smallmatrix}x\\y\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c864cce322545bafba855b5057b9b5e5d547a5d0)
![{\displaystyle {\bigl [}{\begin{smallmatrix}1&0\\0&1\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea62993644c710983784683a626848fcc0baeb20)
![{\displaystyle {\bigl [}{\begin{smallmatrix}1&0\\0&-1\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2f4c8f8efe9d9230f9d29bd79d6f11e64fa8a99)
![{\displaystyle {\bigl [}{\begin{smallmatrix}-1&0\\0&1\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b76e153698ed6b55d0e72c912ec3014014eb8b4)
![{\displaystyle {\bigl [}{\begin{smallmatrix}0&1\\1&0\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22789670a06a228708d442af6830625fae164778)
![{\displaystyle {\bigl [}{\begin{smallmatrix}0&-1\\-1&0\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a25b392c514e9641a899294925aa59089fd42846)
![{\displaystyle {\bigl [}{\begin{smallmatrix}0&1\\-1&0\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2b43c22c71bd785b8e76b7d98fb7ff7348aa781)
![{\displaystyle {\bigl [}{\begin{smallmatrix}-1&0\\0&-1\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1502c26edb8c2f1dd87bd5e23af819e8e07d2e43)
![{\displaystyle {\bigl [}{\begin{smallmatrix}0&-1\\1&0\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ee42f8cd24fda278a8c0bb411911738ea95424)
Subgroups
D4 has three subgroups of order four, one consisting of its two non-involutory elements and their square (that is, its rotations, for the group's action on a square) and two more generated by two perpendicular reflections.
Each reflection generates an order-two subgroup, and there is one more order-two subgroup generated by the central symmetry (the square of the non-involutory elements).
Normal subgroups
There are four proper non-trivial normal subgroups: The two order-four subgroups are normal, as is the group generated by the central symmetry.
This version of the Cayley table shows one of these normal subgroups, shown with a red background. In this table r means rotations, and f means flips. Because this subgroup is normal, the left coset is the same as the right coset.
Group table of D4 e r1 r2 r3 fv fh fd fc e e r1 r2 r3 fv fh fd fc r1 r1 r2 r3 e fc fd fv fh r2 r2 r3 e r1 fh fv fc fd r3 r3 e r1 r2 fd fc fh fv fv fv fd fh fc e r2 r1 r3 fh fh fc fv fd r2 e r3 r1 fd fd fh fc fv r3 r1 e r2 fc fc fv fd fh r1 r3 r2 e The elements e, r1, r2, and r3 form a subgroup, highlighted in red (upper left region). A left and right coset of this subgroup is highlighted in green (in the last row) and yellow (last column), respectively.
See also
References
- ^ Johnston, Bernard L.; Richman, Fred (1997). Numbers and Symmetry: An Introduction to Algebra. CRC Press. p. 92. ISBN 9780849303012.
- ^ Cameron, Peter Jephson (1998). Introduction to Algebra. Oxford University Press. p. 100. ISBN 9780198501954.
- ^ Humphreys, J. F. (1996). A Course in Group Theory. Oxford University Press. p. 47. ISBN 9780198534594.
- ^ Estévez, Manuel; Roldán, Érika; Segerman, Henry (2023). "Surfaces in the tesseract". In Holdener, Judy; Torrence, Eve; Fong, Chamberlain; Seaton, Katherine (eds.). Proceedings of Bridges 2023: Mathematics, Art, Music, Architecture, Culture. Phoenix, Arizona: Tessellations Publishing. pp. 441–444. arXiv:2311.06596. ISBN 978-1-938664-45-8.
External links
- "Dihedral group D8". Groupprops, The Group Properties Wiki.
You must be logged in to post a comment.