Nose cone design

Because of the problem of the aerodynamic design of the nose cone section of any vehicle or body meant to travel through a compressible fluid medium (such as a rocket or aircraft, missile, shell or bullet), an important problem is the determination of the nose cone geometrical shape for optimum performance. For many applications, such a task requires the definition of a solid of revolution shape that experiences minimal resistance to rapid motion through such a fluid medium.

Nose cone shapes and equations

General dimensions

In all of the following nose cone shape equations, $L$ is the overall length of the nose cone and $R$ is the radius of the base of the nose cone. $y$ is the radius at any point $x$ , as $x$ varies from $0$ , at the tip of the nose cone, to $L$ . The equations define the two-dimensional profile of the nose shape. The full body of revolution of the nose cone is formed by rotating the profile around the centerline $C$ ⁄ $L$ . While the equations describe the "perfect" shape, practical nose cones are often blunted or truncated for manufacturing, aerodynamic, or thermodynamic reasons.^[1]^[2]

Conic

Conic nose cone render and profile with parameters shown.

${\begin{aligned}y&={\frac {xR}{L}}=x\tan(\phi )\\\phi &=\arctan \left({\frac {R}{L}}\right)\\\end{aligned}}$

Spherically blunted conic

Spherically blunted conic nose cone render and profile with parameters shown.

${\begin{aligned}x_{t}&&&={\frac {r_{n}L^{2}}{R}}{\sqrt {\frac {1}{R^{2}+L^{2}}}}\\y_{t}&={\frac {x_{t}R}{L}}&&=r_{n}L{\sqrt {\frac {1}{R^{2}+L^{2}}}}\\x_{o}&=x_{t}+{\sqrt {r_{n}^{2}-y_{t}^{2}}}&&=r_{n}\left({\frac {L^{2}}{R}}{\sqrt {\frac {1}{R^{2}+L^{2}}}}+{\sqrt {1-{\frac {L^{2}}{R^{2}+L^{2}}}}}\right)\\x_{a}&=x_{o}-r_{n}&&=r_{n}\left({\frac {L^{2}}{R}}{\sqrt {\frac {1}{R^{2}+L^{2}}}}+{\sqrt {1-{\frac {L^{2}}{R^{2}+L^{2}}}}}-1\right)\\\end{aligned}}$

Bi-conic

Bi-conic nose cone render and profile with parameters shown.

${\begin{aligned}L&=L_{1}+L_{2}\\\phi _{1}&=\arctan \left({\frac {R_{1}}{L_{1}}}\right)\\\phi _{2}&=\arctan \left({\frac {R_{2}-R_{1}}{L_{2}}}\right)\\y&={\begin{cases}{\frac {xR_{1}}{L_{1}}}=x\tan(\phi _{1}),&0\leq x\leq L_{1}\\R_{1}+{\frac {(x-L_{1})(R_{2}-R_{1})}{L_{2}}}=R_{1}+(x-L_{1})\tan(\phi _{2}),&L_{1}\leq x\leq L\end{cases}}\end{aligned}}$

Tangent ogive

Tangent ogive nose cone render and profile with parameters and ogive circle shown.

${\begin{aligned}\rho &={\frac {R-{\frac {L^{2}}{R}}}{2}}\\y&={\sqrt {\rho ^{2}+x(2L-x)}}+\rho \\\end{aligned}}$

Spherically blunted tangent ogive

Spherically blunted tangent ogive nose cone render and profile with parameters shown.

${\begin{aligned}x_{o}&=L-{\sqrt {\left(R-r_{n}\right)\left({\frac {L^{2}}{R}}-r_{n}\right)}}\\y_{t}&={\frac {r_{n}\left(L^{2}-R^{2}\right)}{L^{2}+R^{2}-2Rr_{n}}}\\x_{t}&=L-{\sqrt {\left(R-r_{n}\right)\left({\frac {L^{2}}{R}}-r_{n}\right)}}-r_{n}{\sqrt {1-\left({\frac {L^{2}-R^{2}}{L^{2}+R^{2}-2Rr_{n}}}\right)^{2}}}\\\end{aligned}}$

Secant ogive

Secant ogive nose cone render and profile with parameters and ogive circle shown, ogive radius larger than for equivalent tangent ogive.

For a chosen ogive radius $ρ$ greater than or equal to the ogive radius of a tangent ogive with the same $R$ and $L$ :

${\begin{aligned}\rho &\geq {\frac {R+{\frac {L^{2}}{R}}}{2}}\\\alpha &=\arctan \left({\frac {R}{L}}\right)-\arccos \left({\frac {\sqrt {R^{2}+L^{2}}}{2\rho }}\right)\\y&={\sqrt {\rho ^{2}-(x-\rho \cos \alpha )^{2}}}+\rho \sin(\alpha ),&&0\leq x\leq L\\\end{aligned}}$

Alternate secant ogive render and profile which show a bulge due to a smaller radius.

A smaller ogive radius can be chosen; for ${\textstyle {\frac {1}{2}}\left(R+{\frac {L^{2}}{R}}\right)>\rho >{\frac {L}{2}}}$ , you will get the shape shown on the right, where the ogive has a "bulge" on top, i.e. it has more than one $x$ that results in some values of $y$ .

Elliptical

Elliptical nose cone render and profile with parameters shown.

$y={\frac {R{\sqrt {x(2L-x)}}}{L}}$

Parabolic

A parabolic series nosecone is defined by $r={\tfrac {2x-Kx^{2}}{2-K}}$ where $0\leq x\leq 1$ and $K$ is a series-specific constant.^[3]

Half (

K' = 1/2

)

Three-quarter (

K' = 3/4

)

Full (

K' = 1

)

Renders of common parabolic nose cone shapes.

For $0\leq K'\leq 1$ , $y=R\left({2\left({x \over L}\right)-K'\left({x \over L}\right)^{2} \over 2-K'}\right)$

$K'$ can vary anywhere between $0$ and $1$ , but the most common values used for nose cone shapes are:

Parabola type	$K'$ value
Cone	$0$
Half	$1/2$
Three quarter	$3/4$
Full	$1$

Power series

A power series nosecone is defined by $r=x^{n}$ where $(0\leq x\leq 1)$ . $n<1$ will generate a concave geometry, while $n>1$ will generate a convex (or "flared") shape.^[3]

Half (

n = 1/2

)

Three-quarter (

n = 3/4

)

For

0\leq n\leq 1

:

y=R\left({x \over L}\right)^{n}

Common values of $n$ include:

Power type	$n$ value
Cylinder	$0$
Half (parabola)	$1/2$
Three quarter	$3/4$
Cone	$1$

Haack series

LD-Haack (Von Kármán) (

C = 0

)

LV-Haack (

C = 1/3

)

A Haack series nosecone is defined by:^[3] ${\begin{aligned}r(\theta )&={\sqrt {\frac {\theta -{\frac {1}{2}}\sin(2\theta )+C\sin ^{3}\theta }{\pi }}}\\\theta &=\arccos \!\left(1-2x\right)\\0&\leq x\leq 1\Rightarrow 0\leq \theta \leq \pi \\\end{aligned}}$ where

$r$ is the radius divided by the maximum radius at a given $θ$ or $x$ ,
$x$ is the distance from the nose divided by the total nose length.

Parametric formulation can be obtained by solving the $θ$ formula for $x$ (here, $x$ is now distance from the nose, separated from the total nose length $L$ , and $y$ is the radius). ${\begin{aligned}x(\theta )&={L \over 2}\left(1-\cos(\theta )\right)\\y(\theta ,C)&={R \over {\sqrt {\pi }}}{\sqrt {\theta -{\sin(2\theta ) \over 2}+C\sin ^{3}(\theta )}}\\\end{aligned}}$

Special values of $C$ (as described above) include:

Haack series type	$C$ value
LD-Haack (Von Kármán)	$0$
LV-Haack	$1/3$
Tangent	$2/3$

Von Kármán ogive

The LD-Haack ogive is a special case of the Haack series with minimal drag for a given length and diameter, and is defined as a Haack series with $C = 0$ , commonly called the Von Kármán or Von Kármán ogive. An ogive with minimal drag for a given length and volume can be called an LV-Haack series, defined by $C={\tfrac {1}{3}}$ .^[3] However, the LV-Haack series produces different values for radius as a function of x as opposed to the Sears-Haack body, which also attempts to provide a shape with minimal drag for a given length and volume. For example, the LV-Haack value for radius relative to maximum radius at x=0.5 is ≈ 0.7785, while a Sears-Haack body at the same point (halfway along the nose, which is 25% of the way along the body) has a radius relative to maximum radius of ≈ 0.8059.

Aerospike

An aerospike can be used to reduce the forebody pressure acting on supersonic aircraft. The aerospike creates a detached shock ahead of the body, thus reducing the drag acting on the aircraft.

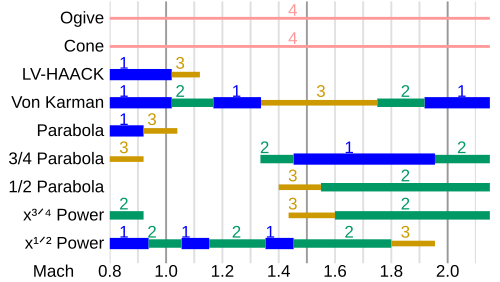
Nose cone drag characteristics

Influence of the general shape

References

^ Crowell Sr., Gary A. (1996). The Descriptive Geometry of Nose Cones (PDF) (Report). Archived from the original (PDF) on 11 April 2011. Retrieved 11 April 2011.
^ satyajit panigrahy (August 2020). "Improvement of Fire Power of Weapon System by Optimizing Nose Cone Shape and War Head Grouping". ResearchGate. doi:10.13140/RG.2.2.28694.36161.
^ ^a ^b ^c ^d Stoney, William E. (February 5, 1954). "TRANSONIC DRAG MEASUREMENTS OF EIGHT BODY-NOSE SHAPES" (PDF). Naca Research Memorandum. NACA-RM-L53K17 – via NASA Technical Reports Server.

[rdp-we-cite_note-crowell-1] Crowell Sr., Gary A. (1996). The Descriptive Geometry of Nose Cones (PDF) (Report). Archived from the original (PDF) on 11 April 2011. Retrieved 11 April 2011.

[rdp-we-cite_note-satyajit-2] satyajit panigrahy (August 2020). "Improvement of Fire Power of Weapon System by Optimizing Nose Cone Shape and War Head Grouping". ResearchGate. doi:10.13140/RG.2.2.28694.36161.

[rdp-we-cite_note-:0-3] Stoney, William E. (February 5, 1954). "TRANSONIC DRAG MEASUREMENTS OF EIGHT BODY-NOSE SHAPES" (PDF). Naca Research Memorandum. NACA-RM-L53K17 – via NASA Technical Reports Server.

[1]

[2]

[3]

KoduKe

Keel

USA, Taani ja Gröönimaa kõnelused Valges Majas läbimurret ei toonud

TÄNA AJALOOS ⟩ Eesti kroon kaotas kehtivuse

A. H. TAMMSAARE ⟩ Kes tahab rohket sigivust, peab astuma võitlusse tehnikaga ja lõbueluga

Euroopa Nõukogu juht hoiatas Ukraina humanitaarkriisi eest

BLOGI ⟩ 1422. sõjapäev Ukrainas: Ukraina vaatab üle komandanditunni reeglid ekstreemse külma ajal

ELU25 ⟩ Juku-Kalle Raid: Teeme nüüd selgeks, kes on ikkagi Kalevipoeg

NIPPE ⟩ Kõhuhädade puhul saab abi taimedest

Ukraina vaatab ekstreemse külma ajal üle komandanditunni reeglid

TEADUSE TERAD ⟩ Haavik on geneetiliselt üksainus organism

Martin Helme hoiatas meelepaha tänavatele valgumise eest